Applications of Integration
Below you will find the exercises we suggest you work on in connection with the Applications of Integration theme and the project problems which are to be done for the exercise classes during October 28 to November 1..
Suggested Exercises
Section 7.1: Volumes by Slicing – Solids of Revolution
7.1.1, 7.1.5, 7.1.7, 7.1.11, 7.1.18.
Relevant pencasts:
Relevant Maple worksheet: :Volumes of revolution
Section 7.2: More Volumes by Slicing
7.2.1, 7.2.15.
Relevant pencasts:
Section 7.3: Arc Length and Surface Area
7.3.1, 7.3.7, 7.3.15, 7.3.23, 7.3.24, 7.3.34, 7.3.37.
Relevant pencasts:
Relevant Maple Worksheet: :Arclength
Section 7.4: Mass, Moments, and Centre of Mass
7.4.1, 7.4.2, 7.4.3, 7.4.4, 7.4.16.
Relevant pencasts:
Relevant Maple worksheet: :Centre of Mass
Section 7.5: Centroids
7.5.1,2, 7.5.15, 7.5.23.
Section 7.6: Other Physical Applications
7.6.1, 7.6.3, 7.6.6.
Section 7.7: Applications in Business, Finance and Ecology
7.7.1, 7.7.9, 7.7.17.
Project Problems
Week 44
These problems are to be presented October 28 to November 1. See here for where you should meet, and here to sign up for presenting a problem.
Problem 1
The triangular region with vertices \((0, -1)\), \((1, 0)\) and \((0, 1)\) is rotated about the line \(x=2\). Find the volume of the region so generated.
Problem 2: Exam 1999 in SIF 5003, problem 3
a) Let \(f(x)=\sqrt{1+x^4}.\) Find the maximal and minimal value of \[f''(x)= \frac{2x^2(x^4+3)}{(x^4+1)^{3/2}}.\]
b) Use the Trapezoid method with 4 subintervals to find an approximation, \(T_4\), to \[I=\int_{0}^{2} \sqrt{1+x^4} \, dx.\] Use problem a) to find the smallest number \(\epsilon\) so that you can guarantee that the error, \(|T_4-I|\), in the Trapezoid approximation used above is less that \(\epsilon\). Hint: -:Numerical Integration.
Explain why the Trapezoid method always gives a bigger value for the above integral, no matter how many subintervals we choose.
Problem 3: Drilling a hole in a sphere
A sphere has radius 5 cm. We drill a hole with radius 3cm through the center of the sphere. We want to calculate the volume of the solid that remains.
a) Show that the volume of the solid that remains can be written as
\[V=4\pi\int_{3}^{5}x\sqrt{5^2-x^2} \, dx.\] Hint: Draw the situation, and :Volumes of revolution.
b) Calculate the volume of the solid.
Problem 4: Exam 1999 in SIF 5003, problem 9
A water tank is made by rotating the graph of the function \(x=g(y)\) about the \(y\)-axis. The volume of the tank at height \(y\) is then given by \[V(y) =\pi\int_{0}^{y}g(u)^2 \, du.\] A hole is made in the bottom of the tank. According to Torricelli's Law the volume then satisfies \[\frac{\mathrm{d}V}{\mathrm{d}t} =-k\sqrt{y},\] where \(y\) is the height of the water and \(k\) is some positive constant.
Determine the function \(g(y)\) when it is given that the change of the height of water per unit time is constant (that is, \(\frac{\mathrm{d}y}{\mathrm{d}t}\) is constant.) and the volume \(V\) is 1 when \(y=1\).
Week 45
These problems are to be presented November 4-8. See here for where you should meet, and here to sign up for presenting a problem.
Problem 1: Maple TA
The semicircular plate \(x^2+y^2 \leq a^2\), \(y \geq0\) has mass \(m=4\pi\) and center of mass in \( (0, \frac{3}{\pi}) \). If the density at a distance \(s\) from the origin is given by \( \rho(s) =ks\), find \(k\) and the radius \(a\).
Hint: Example 2, page 418 in Adams, and :Centre of Mass.
Problem 2:Exam 1997 in SIF 5003, problem 4
Define the function \(F\) by \[F(x) =\int_{1}^{x}\sqrt{t^3-1}\, dt, \] for \(x \geq 1\).
a) Find the length of the curve \(y =F(x)\) when \(1\leq x\leq 2\). Hint: :Arclength.
b) Find the area of the object we get when we revolve the curve from a) about the line \(x=1\).
Problem 3: Swimming Pool
a) A pool 20 m long and 8 m wide has a sloping plane bottom so that the pool is 1 m deep at one end and 3 m deep at the other end. Find the total force exerted on the bottom if the pool is full of water.
b) Find the total work that must be done to pump all the water out of the pool.
Problem 4: Exam 2002 in SIF 5003, problem 5
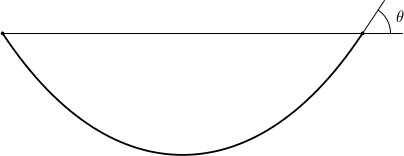
a) Let \(a\) be a positive constant. Find the length of the curve \[y=\frac{\cosh{ax}}{a} \] for \(-1\leq x\leq 1\).
b) Explain why the equation \(x\tanh{x}=1\) has exactly one positive solution \(x_0\). Use Newton's Method to find an approximation to \(x_0\).
c)
The curve in problem a) describes a cable of uniform thickness and density which is hanging freely between two points, as illustrated below.
The tensile force (strekkraften) on the cable in the point \(x=1\) equals half the weight of the cable divided by \(\sin{\theta} \), where \(\theta \) is the angle marked on the figure.
What value of \(a\) gives the least tensile force in the point \(x=1\)? How far down does the midpoint of the cable hang, compared to the end points?