Master projects at SINTEF Applied Mathematics and Cybernetics

General background
The Applied Computational Science group at SINTEF Digital in Oslo focuses on development of numerical methods for solving nonlinear PDEs with applications for real-life geoscience and energy problems. To advance industry-standard simulation technology, we conduct basic research on new numerical methods but more often work on algorithmic improvements that enable the use of more advanced grids and physical models.
We are renowned for our open-source software, which is used all over the world. MRST is a unique software platform for rapid prototyping and testing of new methods and modeling concepts, whereas OPM Flow, which we develop jointly with Equinor and Norce, is an open-source simulator for commercial use.
Writing a master thesis with our group enables you to work with advanced numerical methods for PDEs, but can also give you the possibility to learn more about many other useful topics including professional software development, fully differentiable simulators, nonlinear optimization, and various real-life applications.
In the following we will outline specific proposals that are all related to ongoing research activities in our group. In general, we look for students who are independent and hard-working and who want to be part of a thriving research group consisting of approximately 15-20 researchers. Almost all the proposed projects will enable you to work at the international research front.
At the end of this page, a list of the previous master thesis done in the group is presented, which should help to get an idea of the type of projects we propose.
Contact: Knut [dash] Andreas [dot] Lie [at] sintef [dot] no or Xavier [dot] Raynaud [at] sintef [dot] no (who will act as NTNU-internal supervisors for any of the proposed projects)
Efficient simplified ocean models for oceanographic forecasting
Forecasting of drift trajectories in the ocean serves as an important tool in search-and-rescue operations, planning of oil spill clean-up, and risk assessment for off-shore installations. The Meteorological Institute (Met) has the operational responsibility for doing such forecasting today. The operational approach is to run a single deterministic ocean model to obtain hourly values for 3D currents, temperature, and salinity, and then afterwards make drift forecasts using the outputted surface velocities from this model.
As a complementary approach, we have along with Met developed a GPU-accelerated simplified ocean model based on the rotational shallow water equations (see https://github.com/metno/gpuocean). These equations form a hyperbolic conservation law for mass and (vertically integrated) momentum. The motivation is to trade some physical accuracy against the ability to run (large) ensembles for estimating the uncertainty associated with the drift forecasts. Our model can run on realistic domains by using initial and boundary conditions from the operational 3D ocean model forecast. Additionally, we develop and test various data assimilation methods for updating the (ensemble of) simplified models with available observations.

Modeling approaches
Two-layered shallow-water model
We investigate the use of two-layered shallow-water equations as a simplified ocean model, where two shallow water models are stacked on top of each other. The main challenge with the two- (or many-) layered shallow water equations is that in cases with large shear stress between the layers, the equations are no longer hyperbolic. The project might focus on one or more of the following:
- Efficient implementation of suitable numerical methods on GPUs,
- How to deal with (or avoid) loosing hyperbolicity in realistic applications,
- Initialization from operational models to simulate realistic domains and drift trajectories along the Norwegian coast.
Thermal rotational shallow-water model
We investigate the use of thermal rotational shallow-water equations as a simplified ocean model for drift trajectory prediction. This model includes density as an additional variable, and thereby incorporates some of the physics that we have previously neglected. The project will consist of developing a GPU-accelerated solver for these equations and compare it to the model we use today. Contact: havard.heitlo.holm@sintef.no
Contact: havard [dot] heitlo [dot] holm [at] sintef [dot] no
Modeling and Optimization of Underground Hydrogen Storage
The significance of hydrogen as an energy carrier and its role in renewable energy integration have grown substantially in recent years. With its potential to store surplus energy generated from intermittent renewable sources like wind and solar power, hydrogen storage provides an effective means to balance energy supply and demand. Hydrogen's versatility extends to various sectors, including transportation, industry, and heating, making it a cornerstone of sustainable energy systems.
In particular, Underground Hydrogen Storage (UHS) plays a pivotal role in the quest for efficient renewable energy utilization and the assurance of a consistent energy supply. However, realizing the full potential of UHS necessitates the development of optimized strategies and operational protocols.
This master proposal seeks to enhance the safety and sustainability of hydrogen storage operations by efficiently optimizing storage-withdrawal cycles, injection rates, and control strategies. The overarching goal is to maximize storage efficiency through the optimization of Injection-Idle-Withdrawal (I-I-W) cycles, which involve varying net ramping rates and bottom-hole pressure (bhp) control, periodicities, and stand-by periods. All these enhancements are pursued while steadfastly adhering to the critical assumption that the capillary entry pressure within the caprock must never be exceeded. Additionally, we aim to prevent the occurrence of upconing phenomena at the gas-water interface during withdrawal, ensuring that hydrogen production aligns with the dynamically changing requirements of the highly flexible hydrogen market.


Objectives
Development of Reduced-Order Models
Our primary objective is to create and experiment with reduced-order models derived from detailed fine-scale flow simulations. These models will comprehensively describe hydrogen behavior during injection, withdrawal, and idle periods within underground storage facilities. Factors such as capillary entry pressure, reservoir characteristics, and upconing effects will be incorporated into these models. The reduced-order models will act as computational shortcuts that retain these essential features of the system, allowing us to perform optimization tasks at a fraction of the computational cost compared to traditional reservoir simulators.
Designing Control Strategies
Once we have developed one or more reduced models (Graph-based, Proxy, Flow-Diagnostics models,..) and selected operational parameters (Injection rate, periodicity, times, etc..), our focus will shift to designing advanced control strategy algorithms to efficiently optimize these parameters while upholding safety and environmental standards. This includes
Enhancing Storage Efficiency
The goal is to determine optimal net ramping rates during the injection phase to ensure that the storage zone remains within safe pressure limits, avoiding the risk of hydrogen leakage through the caprock while maximizing storage capacity. Similar considerations will apply during withdrawal to prevent rapid depressurization and upconing of the gas-water interface.
Optimizing Stand-By Periods and balancing Periodicities
The goal is to optimize the timing of injection, idle, and withdrawal periods to identify the most suitable rhythm for UHS. These phases are crucial for maintaining stable pressure conditions within the storage facility and reducing the potential for upconing phenomena. Recognizing the need for stand-by periods during hydrogen storage, we will optimize the duration and frequency of these periods to ensure minimal energy wastage and rapid response to changing demand. These considerations will aid in establishing the maximum allowable hydrogen injection and production rates for the underground storage zone, ensuring safe pressure levels are maintained while optimizing storage capacity.
Learning outcomes
This project involves gaining expertise in essential areas, such as flow models and the associated numerical and computational mathematics, with the aid of tools like the MATLAB Reservoir Simulation Toolbox (MRST). Furthermore, it encompasses proficiency in optimization and adjoint algorithms to address constrained flow models and optimize operational parameters and control strategies.
Contact: elyes [dot] ahmed [at] sintef [dot] no, olav [dot] moyner [at] sintef [dot] no
Modeling and simulation of Electro-chemical systems
Li-ion Battery
Batteries play an essential role towards an emission-free energy supply. Simulation tools for batteries are developed for data analysis and performance prediction. They are also used for design (new chemistry and geometries) and operation (battery management systems) optimization.
In our group, we develop open source simulation tools for battery cell simulation. We propose projects with a strong flavor of mathematical modeling and numerical implementation. The topics we propose now are
Battery degradation
Lithium plating and solid electrolyte growth are identified as the primary degradation mechanisms in Li-ion batteries. The goal of the project is to integrate these processes that are more or less understood at the microscopic level to the macroscopic level where the impact on the battery operation is measured.
Silicon swelling
Because of its high capacity, Silicon is an attractive electrode material. A major drawback is the large deformation of Silicon depending on the Lithium content (up to 300% swelling). By design, batteries are developed for cyclic operations. The alternation of swelling and depletion induces therefore a stress that is detrimental to the battery integrity.
In this project, we want to couple the mechanisms aspects of Silicon swelling with the electro-.chemical model and implement a code that can predict the overall impact on the battery performance.
Hydrogen production
The production of hydrogen by water electrolysis is critical for an emissions-free energy system. Water electrolysis with renewable electricity can make pure hydrogen without using fossil fuels or producing greenhouse gases. The cost of water electrolysis, however, is still too high to be economically viable.
Improvements in electrolyser efficiency and durability could reduce operating and capital costs. Additionally, many renewable electricity sources, like wind turbines and solar panels, are intermittent, so coupling these sources to an electrolysis system may require that system to operate dynamically depending upon the electricity supply.
Computational models for electrolyser cells and stacks can provide guidance in terms of optimal system operation and design, as well as deriving greater understanding of the physical processes happening inside an electrolysis cell.
In this project, the plan is look at one of the following mechanisms, derive the modeling equations and implement a numerical code to evaluate the models.
Membrane degradation
A key concern in electrolysis is the degradation of the membrane over time. Performance decreases and durability restrictions are mostly due to membrane pollution or degradation. An example of pathways for degradation is
- Oxygen crossover through the membrane from anode to cathode side, facilitated by water flow, in which the gas is dissolved.
- Production of H2O2 at the cathode.
- Formation of free radicals, with or without the presence of Fenton-active metal ions (in this case Fe2+ ).
- Subsequent attack on the membrane resulting in fluorine release and membrane thinning.
Gas Bubble formation
Gas bubbles can reduce the available surface area of the catalyst that is electrochemically available by blanketing the catalyst, preventing water transport to the site. In systems with a liquid electrolyte, gas bubbles can also impede solute transport, resulting in reduced effective conductivity of the electrolyte.
Contact: xavier [dot] rayanaud [at] sintef [dot] no, august [dot] johansson [at] sintef [dot] no
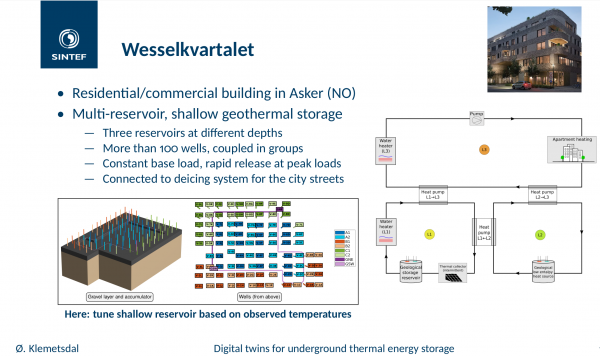
Geothermal Energy
Hybrid, graph-based methods for partial differential equations
Numerical solutions to partial differential equations (PDEs) require a discrete formulation of the continuous problem. For many numerical methods, this discrete formulation can be thought of as a graph: in finite-volume methods, for example, the grid cells represent nodes, whereas cell interfaces represent edges, and their assigned weights (and model parameters) are determined by the underlying physical description and the discretization.
To reduce the number of unknowns, one can coarsen a simulation graph by aggregating nodes and tune the parameters of this coarse graph so that the coarse model matches the underlying fine-scale model. In this project, the student will work on finding optimal, graph-based methods for PDEs, particularly focusing on three aspects:
- For a given simulation model, workflow and a computational budget, find the optimal coarse discretization graph topology.
- Given a parameterized discretization graph, efficiently optimize its node and edge parameters so that the model best matches observed data.
- Each node in the discretization graph contains a set of primary variables, constitutive laws, and functional relationships for deriving properties and equation residuals. Accordingly, each node itself contains a computational graph that also can be pruned (e.g., by simplifying the physics) in an optimized manner.
Throughout the project, the student will gain valuable knowledge in both physics-based and data-driven modeling, graph theory, as well as continuous optimization techniques that fuel the training process in many neural network architectures. The graph-based approach represents a very promising physics-informed alternative to machine learning.
Contact: knut [dash] andreas [dot] lie [at] sintef [dot] no, oystein [dot] klemetsdal [at] sintef [dot] no, stein [dot] krogstad [at] sintef [dot] no

Conforming Voronoi grids
Polytopal grids (consisting of polygons in 2D or polyhedra in 3D) are becoming increasingly popular in the numerical solution of partial differential equations because of their ability to adapt to complex geometries while maintaining quality. For example, nonconvex shapes give great flexibility when conforming to internal and external boundaries. General polytopes also enable hanging nodes, which is important for effective mesh refinement.
Despite their popularity, there are not many tools for generation of polytopal grids. The purpose of this project is to start implementing an open-source tool. To this end, the student will develop and implement methods for fast and robust generation of so-called Voronoi grids that adapt to complex geometric constraints, and potentially disseminate it in an open-source software package. Such software can be very useful to a large, scientific community. Through the project, the student will gain knowledge of the mathematics behind advanced meshing algorithms, numerical methods applicable to such grids, and open-source software implementation.
Supervisors: oystein [dot] klemetsdal [at] sintef [dot] no and knut [dash] andreas [dot] lie [at] sintef [dot] no
Illustrations (from left to right) : Voronoi grids conforming to a simple network of intersecting, elliptical planes, generated by the UPR module in SINTEF’s MRST software. An example of a grid generated with VoroCrust, from Sandia National Labs.



Smart cities: Using conservation laws to control traffic lights and speed limits
Road congestion is a common problem in modern cities, and several approaches are being tried to amend the issue. In this project, we propose a mathematical approach for finding settings for traffic lights and speed limits that optimizes traffic flow. The approach is flexible and allows to prioritize optimal settings for parts of the traffic flow, e.g., public transport.
You will utilize non-linear conservation laws to model traffic density, and use integer programming (optimization where the parameters are bound to be integers) to determine the best possible configuration.
This project is a key component in making smart cities – smart cities need smart traffic control.
Learning outcomes
- Fundamentals for numerical solutions of scalar non-linear conservation laws
- Integer optimization
- (Optional) High-performance computing for fast solutions of the conservation law
- (Optional) Data-assimilation for priming the model with observed traffic density

Contact: Kjetil [dot] Olsen [dot] Lye [at] sintef [dot] no and Franz [dot] Fuchs [at] sintef [dot] no
Advanced solvers for specific applications
The equations governing flow in porous rocks consist of a coupled set of nonlinear PDEs that typically are discretized using a fully-implicit, finite-volume method. The most common way of solving the resulting nonlinear system of discrete equations is to use some variant of Newton-Raphson’s method, which is robust and has good convergence properties. To implement Newton’s method, one typically needs to compute Jacobians of residual equations (conservation of mass between computational cells, conservation of energy over interfaces etc). For systems of equations this can quickly become cumbersome even though the derivations are relatively simple. Automatic differentiation is a technology that, at runtime, automatically computes all relevant derivatives according to a simple set of rules. The result is solvers that are easy to modify and maintain. MRST and OPM both have libraries for automatic differentiation that makes it easy to switch between different solvers for both the linear and nonlinear problems.
Numerical simulation of fracture formations on irregular grids, using phase field and virtual element methods
A fracture is formed along a surface, when the stress that is exerted on the rock exceeds the energy required to break the cohesion of the rock along the surface. The fractures are two-dimensional objects and the difficulty is to identify the surfaces that eventually become the support of fractures. Phase-field methods bring a solution to this problem by introducing a variable field that measures the damage of the material and the location of fractures are then identified as the regions where the phase field variable takes its maximum possible value. Elliptic partial differential equations of second or fourth order are used to model the evolution of the phase field variable. In this project, the student is invited to study and implement numerical schemes to solve these partial differential equations and couple them with the linear elasticity equations that model the behavior of the unfractured rock. In order to obtain methods that are compatible with the grids that are used in reservoir simulation, the implementation will be done using virtual elements methods as they are able to handle irregular grids.
CO2 Sequestration
The net European CO2 emissions from energy industries, manufacturing, and production totaled 1.95 Gt in 2011. Ongoing Carbon Capture and Storage (CCS) operations typically inject 1-2 Mt per year. To make a significant impact on climate, one needs to significantly scale up the injection operations and store hundreds of megatonnes each year. Sedimentary basins offshore Norway contain a number of saline aquifers with large volumes of pore space potentially usable for CO2 storage of this magnitude. The Norwegian Petroleum Directorate (NPD) has released two CO2 Storage Atlases that explore large-scale CO2 storage for a number of aquifers. In total, twenty-seven geological formations have been grouped into aquifers whose qualities are assessed with regard to CO2 storage potential.
At SINTEF, we have developed MRST-co2lab (http://www.sintef.no/co2lab) which offers a set of novel simulation tools that can be used to simulate likely outcomes of large-scale, long-term migration processes and estimate capacity for large-scale structural, residual, and solubility trapping. The tools have, in particular, been used to develop plausible plans for injecting hundreds of megatonnes of CO2 into the Utsira and Skade formations. However, the studies performed so far have been cursory and only intended to demonstrate the capabilities of the numerical methods. In the project, the student(s) will perform a more in-depth study that includes critical evaluation of various model assumptions (boundary conditions, etc) and focus on providing capacity estimates with a high degree of realism. More details available upon request
Previous Master Thesis
Bendik S. Waade
Numerics-informed neural networks and inverse problems with hyperbolic balance laws (2023)
Advisors: K.O. Lye and E.R. Jakobsen
Ingvild S. Devold
Hybrid, graph-based methods for reduced-order and data-driven reservoir modeling (2023)
Advisors: K.A. Lie and S. Krogstad and Ø. Klemetsdal
Sondre Husøy
Constrained generation of Voronoi meshes using inscribed sphere distance (2023)
Advisors: K.A Lie and A. Johansson and Ø. Klemetsdal
Vetle Nevland
An extended fully-implicit hybrid model for geological CO2 storage (2023)
Advisors: K.A. Lie and O. Andersen and H. Hellevang
Duy Duc Khuat
Improved optimization methods for adjoint-based training of reduced-order models (2022)
Advisors: K.A. Lie and S. Krogstad
Anders Håøy Rokne
Quantum error mitigation for CNOT-gates (2021)
Advisors: K.A. Lie and F.G. Fuchs and J. Danon
Marius C. Landsverk
Inductive bias and the information bottleneck method (2021)
Advisors: K.A. Lie and S. Riemer-Sørensen
Thibault Edward Gaudet
Upscaling the effect of thin low-permeability shale layers on the vertical migration of CO2. (2020)
Advisors: K.A. Lie
Mona-Lena Norheim
Investigating iterative solvers of Poisson-type equations discretized by the two-point flux-approximation scheme (2019)
Advisors: K.A. Lie and O. Møyner
Sindre Grøstad
Automatic differentiation in Julia with application to numerical solution of PDEs (2019)
Advisors: K.A. Lie and O. Møyner and A.F. Rasmussen
Ferenc Szekely
Mathematical modeling and numerical study of viscous fingering (2018)
Advisors: X. Raynaud and H.M. Nilsen
Pia-Kristina Heigrestad
Nonlinear two-point flux approximation schemes (2018)
Advisors: K.A. Lie and O. Møyner
Raymond Toft
Two-phase reservoir simulation with the full approximation scheme (2018)
Advisors: K.A. Lie and O. Møyner
Roman Bohne
Machine-learning algorithms for the computation of upscaled permeabilities (2018)
Advisors: K.A. Lie and X. Raynaud
Håkon Jarvis Westergård
Fast marching and fast sweeping in optimal path planning (2018)
Advisors: K.A. Lie and S. Zahedi and S. Krogstad
Anders Opskar Voldsund
A mathematical model for calculating river hydrographs using high resolution digital elevation models (2017)
Advisors: K.A. Lie and A. Brodtkorb and O. and ersen
Fredrik Johannesen
Accelerated computation with the multiscale restriction-smoothed-basis method on distributed memory systems (2016)
Advisors: K.A. Lie and O. Møyner
Andreas Almlien Røssland
PRST - Python Reservoir Simulation Toolbox (2016)
Advisors: K.A. Lie and O. Møyner
Ingeborg Gjerde
Simulations of underground storage of natural gas (2016)
Advisors: K.A. Lie and H.M. Nilsen
Runar Lie Berge
Unstructured PEBI grids adapting to geological features in subsurface reservoirs (2016)
Advisors: K.A. Lie
Magnus Jordstad
Multigrid preconditioning of linear elasticity in anisotropic porous media (2016)
Advisors: K.A. Lie and T. Kvamsdal
Stine Vennemo
Multiscale simulation of thermal flow in porous media (2016)
Advisors: K.A. Lie and O. Møyner
Swej Shah
The multiscale restriction smoothed basis method for fractured porous media (2015)
Advisors: K.A. Lie
Aleksander Amundsen
Microbial enhanced oil recovery - modeling and numerical simulations (2015)
Advisors: K.A. Lie and X. Raynaud and S.M. Nielsen
Henrik Vikøren
Towards a parallel multiphase solver based on potential ordering (2015)
Advisors: K.A. Lie
Jens Kristoffer Reitan Markussen
An open-source framework for solving hyperbolic conservation and balance laws on GPUs (2015)
Advisors: K.A. Lie
Cecilia Halmøy
Estimation of pressure propagation in reservoirs using the fast-marching method (2015)
Advisors: K.A. Lie
Guro Seternes
Simulations of CO2 migration with a fully-integrated VE model on the GPU (2015)
Advisors: K.A. Lie and H.M. Nilsen and A. Brodtkorb
Tor Gramann Nærland.
Accelerating Reactive Transport Modeling (2015)
Advisors: K.A. Lie and A. Brodtkorb
Svein Morten Drejer
Optimal non-linear solvers: applications in reservoir simulation (2014)
Advisors: K.A. Lie and H. Holden
Thea Knudsen
Full implicit WENO scheme for two phase flow in reservoir simulation. (2014)
Advisors: K.A. Lie and H. Holden and X. Raynaud
Kristin A. Larssen
Steady-state upscaling of polymer flow (2013)
Advisors: K.A. Lie and Daniel W. Schmid and Marcin Dabrowski
Espen Graff Berglie
Higher-order methods for the shallow-water equations on GPUs. (2013)
Advisors: K.A. Lie and H. Holden and A.R. Brodtkorb
Are Gabriel Høyland
Multiscale methods in reservoir simulation (2012)
Advisors: K.A. Lie and H. Dahle
Jens Birkevold
Divergence-free isogeometric methods for flow in porous media (2012)
Advisors: K.A. Lie and T. Kvamsdal
Ruben Bø
Mimetic discretizations on grids with curved surfaces (2012)
Advisors: K.A. Lie and S. Krogstad and H. Holden
Simen Lønsethagen
Krylov subspace accelerated algebraic multigrid for mimetic finite differences on GPUs (2012)
Advisors: K.A. Lie and B. Skaflestad and H. Holden
Anders Hoff
A parallel multiscale mixed finite element method for the Matlab Reservoir Simulation Toolbox (2012)
Advisors: K.A. Lie and B. Skaflestad and H. Holden
Christine M. Ø Haugland
Applying hybrid methods to reduce nonphysical cycles in the flux field (2012)
Advisors: K.A. Lie and S. Krogstad and H. Holden
Olav Møyner
Multiscale finite-volume methods on unstructured grids (2012)
Advisors: K.A. Lie and B. Skaflestad and H. Holden
Lars Jahr Røine
Visualization of subsurface grids in Octave (2012)
Advisors: K.A. Lie and C. Dyken
Martin Ertsås
Vertically integrated models of CO2 migration: GPU accelerated simulations (2011)
Advisors: K.A. Lie and J. R. Natvig and M. Reimers
Karianne H. Christensen
Adaptive Voronoi grids in the MATLAB Reservoir Simulation Toolbox (2010)
Advisors: K.A. Lie and J.R. Natvig and H. Holden
Gagandeep Singh
Mimetic finite difference method on GPU. Application in reservoir simulation and well modeling. (2010)
Advisors: K.A. Lie and B. Skaflestad and T. Kvamsdal
Audun Torp
Sparse linear algebra on a GPU (with applications to flow in porous media) (2009)
Advisors: K.A. Lie and T. Kvamsdal
Asbjørn Bydal
GPU-accelerated simulation of flow through porous mediumi (2009)
Advisors: K.A. Lie and T.R. Hagen and O.-C. Granmo
Ingeborg Skjelkvåle Ligaarden
Well models for mimetic finite difference methods and improved representation of wells in multiscale methods (2008)
Advisors: K.A. Lie and S. Krogstad
Lars Moastuen
Real-time simulation of the incompressible Navier-Stokes equations on the GPU (2007)
Advisors: K.A. Lie and T.R. Hagen
Martin Lilleeng Sætra
Solving systems of hyperbolic PDEs using multiple GPUs (2007)
Advisors: K.A. Lie and T.R. Hagen
Andre Rigland Brodtkorb
A Matlab interface to the GPU (2007)
Advisors: K.A. Lie and T.R. Hagen
Trygve Fladby
Efficient linear algebra on heterogeneous processors (2007)
Advisors: K.A. Lie and T.R. Hagen
Thomas Lunde
Comparison between mimetic and two-point flux-approximation schemes on PEBI-grids (2007)
Advisors: K.A. Lie and J.E. Aarnes
Hanne Moen
Wavelet transforms and efficient implementation on the GPU (2007)
Advisors: K.A. Lie and T.R. Hagen
Ola Iver Røe
Discontinous Galerkin methods with optimal ordering for fast reservoir simulation on unstructured tetrahedral grids. (2006)
Advisors: K.A. Lie and J.R. Natvig and H. Holden
Jan-Frode Stene
Central difference schemes for gas dynamics (2003)
Advisors: K.A. Lie and H. Holden
Kjetil Bergh-Ånonsen
Central difference schemes for gas dynamics (2003)
Advisors: K.A. Lie and H. Holden
Vegard Kippe
Streamline methods for reservoir simulation (2003)
Advisors: K.A. Lie and H. Holden
Thomas F. Skjønhaug
Finite volume methods for the two-phase pressure equation (1999)
Advisors: K.A. Lie and A. Tveito
Jostein R. Natvig
Front tracking and operator splitting methods for the polymer system (1998)
Advisors: K.A. Lie and H. Holden and K. H. Karlsen
Runar Holdahl
Front tracking and operator splitting methods for the shallow water equations (1998)
Advisors: K.A. Lie and H. Holden