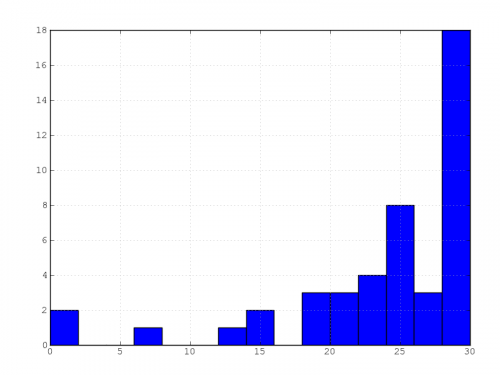
Results
Here are the final grades for the project. Note that the project gives a maximum 30 points out of the 100 points for the total grade. Note also that no matter the project grade, you still need to get at least 28/70 points (40%) in the final exam to pass the course.
Note that there were some errors in the project grades published last thursday. Hopefully, those errors are now fixed.
| Nr | Grade/30 |
|---|---|
| 634938 | 0 |
| 654178 | 16 |
| 683942 | 27 |
| 698244 | 22 |
| 699049 | 26 |
| 705352 | 12 |
| 705428 | 24 |
| 705442 | 24 |
| 705708 | 30 |
| 707750 | 30 |
| 707767 | 24 |
| 707905 | 26 |
| 712651 | 8 |
| 715007 | 30 |
| 715066 | 20 |
| 716038 | 30 |
| 716438 | 12 |
| 716439 | 20 |
| 716443 | 28 |
| 716455 | 22 |
| 716460 | 15 |
| 716464 | 20 |
| 716467 | 28 |
| 716475 | 15 |
| 716486 | 30 |
| 716488 | 30 |
| 717867 | 21 |
| 719306 | 30 |
| 722284 | 30 |
| 722301 | 30 |
| 722380 | 28 |
| 722382 | 27 |
| 722386 | 30 |
| 722390 | 21 |
| 722391 | 25 |
| 722392 | 30 |
| 722393 | 25 |
| 722397 | 30 |
| 722398 | 28 |
| 722399 | 28 |
| 722401 | 21 |
| 724006 | 22 |
| 728394 | 27 |
| 728529 | 22 |
| 728628 | 22 |
| 730838 | 30 |
| Date | Return date | Assignment | |
|---|---|---|---|
| 2012-02-16 | 2012-03-08 | Project |
LaTeX
If you want to typeset the project with LaTeX, you may use the following template to get started. This include
- Neville and Divided Difference tables
- Interpolation tables
- Graphs
- Python and Matlab code
Download it here: LaTeX Template
For other help and introduction to LaTeX you may consult the LaTeX wikibook.
Polynomial Interpolation with polyfit and polyval
I describe here usage of polyfit and its close friend polyval.
To obtain an interpolating polynomial, you would go as follows:
p = polyfit([0.,2.,1.], [2.,1.,1.], 2)
Do not forget the third argument, which is the degree of the polynomial that you wish to interpolate with. You should always use the number of interpolation points minus one (here 2 = 3-1).
Now that you have the polynomial p, you may evaluate it at various points as follows
polyval(p, 10) # value of the polynomial at x = 10
This is especially useful if you want to plot a polynomial. You would go as follows:
xs = linspace(-1,3,500) # 500 points between -1 and 3 ys = polyval(p, xs) # the y values plot(xs,ys)